为什么 90% 的回测失败

大约十分之九的回测会产生错误或误导性的结果。这是精心开发的算法交易系统经常在实时交易中失败的第一个原因。即使使用样本外数据，甚至使用交叉验证或前向分析，回测结果也往往偏向乐观。大多数具有正面回测的交易系统实际上都是无利可图的。在本文中，我将讨论这种现象的原因，以及如何解决它。

假设您正在开发一种算法交易策略，遵循正确系统开发的所有规则. 但是您不知道您的交易算法没有统计优势。该策略毫无价值，交易规则等同于随机交易，除交易成本外，预期利润为零。问题：你很少会在回测中得到零结果。随机交易策略将在 50% 的情况下产生负面的回测结果，在 50% 的情况下产生正面结果。但是，如果结果是否定的，您通常很想调整代码或选择资产和时间框架，直到最终获得有利可图的回测。即使对系统进行随机修改，这种情况也会相对较快地发生。这就是为什么周围有这么多无利可图的策略，但回测表现却很好。

这是否意味着回测毫无价值？一点也不。但重要的是要知道您是否可以信任该测试。

回测实验

有几种方法可以验证回测。它们都不是完美的，但都从不同的角度给出了见解。我们将使用Zorro 算法交易软件，并使用以下测试系统运行我们的实验，该测试系统已通过前向分析进行了优化和回测：

function run()
{
  set(PARAMETERS,TESTNOW,PLOTNOW,LOGFILE);
  BarPeriod = 1440;
  LookBack = 100;
  StartDate = 2012;
  NumWFOCycles = 10;

  assetList("AssetsIB");
  asset("SPY");

  vars Signals = series(LowPass(seriesC(),optimize(10,2,20,2)));
  vars MMIFast = series(MMI(seriesC(),optimize(50,40,60,5)));
  vars MMISlow = series(LowPass(MMIFast,100));

  MaxLong = 1;
  if(falling(MMISlow)) {
    if(valley(Signals))
      enterLong();
    else if(peak(Signals))
      exitLong();
  }
}

这是一个经典的趋势跟踪算法。它使用低通滤波器在平滑价格曲线的波峰和波谷进行交易，并使用 MMI 滤波器（市场均值指数）来区分趋势和非趋势市场时期。它仅在市场切换到rend 制度时进行交易，这对于盈利的趋势跟踪系统至关重要。它只打开多头头寸。优化了低通和 MMI 滤波器周期，回测是10 个周期的前向分析。

安慰剂交易系统

将真实材料与安慰剂进行比较是实验的标准。为此，我们使用的交易系统显然没有优势，但出于恶意目的进行了调整，以在前瞻分析中显示为有利可图。这是我们的安慰剂系统：

void run()
{
  set(PARAMETERS,TESTNOW,PLOTNOW,LOGFILE);
  BarPeriod = 1440;
  StartDate = 2012;
  setf(TrainMode,BRUTE);
  NumWFOCycles = 9;

  assetList("AssetsIB");
  asset("SPY");

  int Pause = optimize(5,1,15,1);
  LifeTime = optimize(5,1,15,1);

// trade after a pause...
  static int NextEntry;
  if(Init) NextEntry = 0;
  if(NextEntry-- <= 0) {
    NextEntry = LifeTime+Pause;
    enterLong();
  }
}

该系统打开一个头寸，保持一段时间，然后关闭它并暂停一段时间。交易和暂停持续时间在 1 天到 3 周之间进行了优化。LifeTime是一个预定义的变量，在给定时间后平仓。如果您不相信幸运交易模式，您可以正确地假设该系统等同于随机交易。让我们看看它与趋势交易系统相比如何。

趋势交易与安慰剂交易

这是从 2012 年到 2022 年 3 月前瞻分析的趋势交易系统的股票曲线：

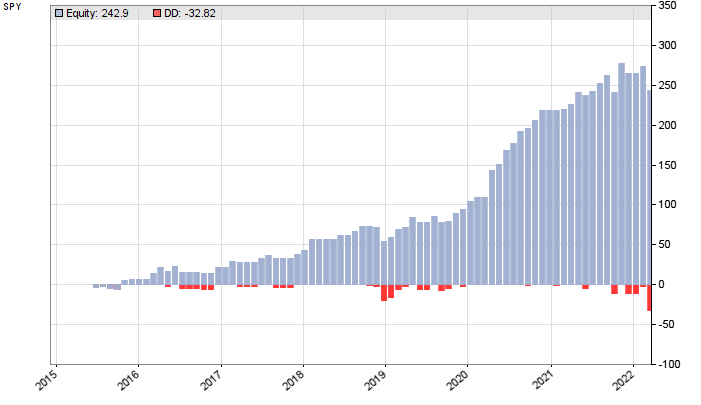
该图从 2015 年开始，因为前 3 年用于训练和回溯期。SPY 跟随标准普尔 500 指数并长期上涨，因此我们无论如何都可以期望通过只做多的系统获得一些利润。但是这个系统，利润因子为 3，R2 系数为 0.65，似乎比随机交易好很多。让我们将其与安慰剂系统进行比较：

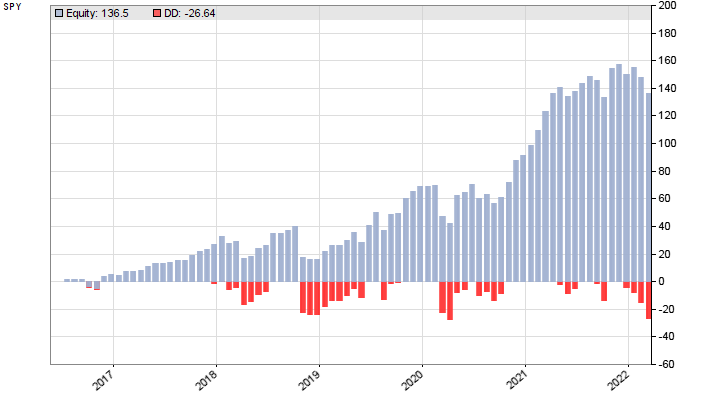
安慰剂系统产生利润因子 2 和 R2 系数 0.77。略低于真实系统，但在相同的性能范围内。这个结果也来自前向分析，尽管有 9 个周期——因此是测试期的较晚开始。除此之外，似乎不可能仅从资产曲线和绩效数据中确定哪个系统是真实的，哪个是安慰剂。

检查现实

验证回测结果的方法称为“现实检查”。它们特定于资产和算法；在多资产、多算法组合中，您只需启用要测试的组件。我们先来看看 WFO 拆分如何影响回测。通过这种方式，我们可以找出我们的回测结果是否只是由于特定 WFO 周期中的幸运交易。我们将绘制一个WFO 配置文件，以显示步进循环次数对结果的影响。为此，我们将代码中的NumWFOCycles = …行注释掉，并使用WFOProfile.c脚本在训练模式下运行它：

#define run strategy
#include "trend.c" // <= your script
#undef run
#define CYCLES 20 // max WFO cycles

function run()
{
  set(TESTNOW);
  NumTotalCycles = CYCLES-1;
  NumWFOCycles = TotalCycle+1;
  strategy();
}

function evaluate()
{
  var Perf = ifelse(LossTotal > 0,WinTotal/LossTotal,10);
  if(Perf > 1)
    plotBar("WFO+",NumWFOCycles,NumWFOCycles,Perf,BARS,BLACK);
  else
    plotBar("WFO-",NumWFOCycles,NumWFOCycles,Perf,BARS,RED);
}

我们将run函数重新定义为不同的名称。这允许我们只包含测试脚本并使用从 2 到 CYCLES 定义的数字的 WFO 循环对其进行训练。训练后执行回测。如果存在评估函数，Zorro 会在任何回测后自动运行它。它绘制了每个 WFO 周期数的利润因子（y 轴）的柱状图。一、趋势交易系统的WFO简介：

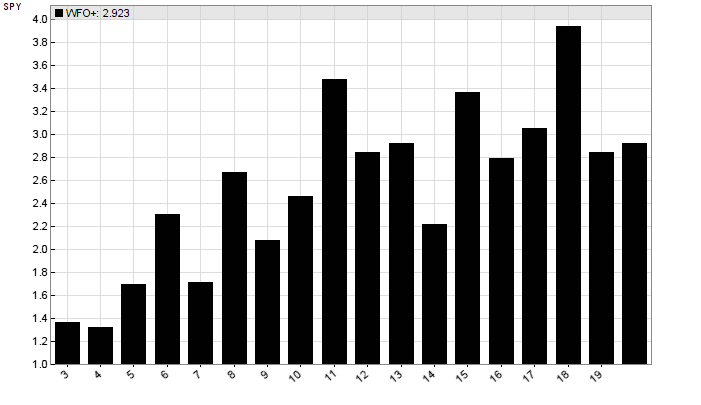
我们可以看到性能随着循环次数的增加而上升。这对于适应市场的系统来说是典型的。所有结果都是正的，利润因子 > 1。我们任意选择 10 个周期产生的结果低于平均水平。所以我们至少可以确定这个回测结果不是由特别幸运的 WFO 周期数引起的。

安慰剂系统的 WFO 概况：

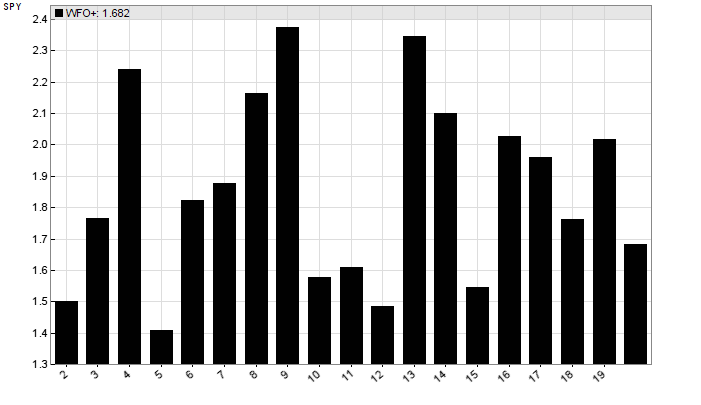
这一次，WFO 周期数对性能产生了强烈的随机影响。现在很明显为什么我为该系统使用了 9 个 WFO 循环。出于同样的原因，我使用了蛮力优化，因为它增加了 WFO 方差，从而有机会获得幸运的 WFO 周期数。这与我们通常在开发算法交易策略时所做的相反。

WFO 配置文件可以深入了解 WFO 周期依赖性，但不能通过其他方式了解随机性或过度拟合。为此，需要进行更深入的测试。Zorro 支持两种方法，即具有随机价格曲线的 Montecarlo Reality Check (MRC)，以及具有策略变体的去趋势和自举资产曲线的White’s Reality Check (WRC)。两种方法都有其优点和缺点。但由于优化策略变体只能在没有前向分析的情况下创建，所以我们在这里使用 MRC。

蒙特卡罗现实检查

首先，我们用随机价格曲线测试这两个系统。随机化消除了短期价格相关性和市场低效率，但保持了长期趋势。然后我们将原始回测结果与随机结果进行比较。这会产生一个p 值，这是我们的测试结果是由随机性引起的概率的度量。p 值越低，我们对回测结果的信心就越大。在统计学中，当 p 值低于 5% 时，我们通常认为结果显着。

Montecarlo Reality Check (MRC) 的基本算法：

1. 训练您的系统并运行回测。存储利润因子（或您要比较的任何其他性能指标）。
2. 通过随机交换价格变化来随机化价格曲线（无替换洗牌）。
3. 使用随机数据再次训练您的系统并运行回测。存储性能指标。
4. 重复步骤 2 和 3 1000 次。
5. 确定结果比原始测试更好的随机测试的数量 N。p 值为 N/1000。

如果我们的回测结果受到整体向上趋势价格曲线的影响，对于这个 SPY 系统来说肯定是这种情况，那么随机测试也会受到影响。MRC代码：

#define run strategy
#include "trend.c" // <= your script
#undef run
#define CYCLES 1000

function run()
{
  set(PRELOAD,TESTNOW);
  NumTotalCycles = CYCLES;
  if(TotalCycle == 1) // first cycle = original
    seed(12345); // always same random sequence
  else
    Detrend = SHUFFLE;
  strategy();
  set(LOGFILE|OFF); // don't export files
}

function evaluate()
{
  static var OriginalProfit, Probability;
  var PF = ifelse(LossTotal > 0,WinTotal/LossTotal,10);
  if(TotalCycle == 1) {
    OriginalProfit = PF;
    Probability = 0;
  } else {
    if(PF < 2*OriginalProfit) // clip image at double range
      plotHistogram("Random",PF,OriginalProfit/50,1,RED);
    if(PF > OriginalProfit)
      Probability += 100./NumTotalCycles;
  }
  if(TotalCycle == NumTotalCycles) { // last cycle
    plotHistogram("Original",
     OriginalProfit,OriginalProfit/50,sqrt(NumTotalCycles),BLACK);
    printf("\n-------------------------------------------");
    printf("\nP-Value %.1f%%",Probability);
    printf("\nResult is ");
    if(Probability <= 1)
      printf("highly significant") ;
    else if(Probability <= 5)
      printf("significant");
    else if(Probability <= 15)
      printf("maybe significant");
    else
      printf("statistically insignificant");
    printf("\n-------------------------------------------");
  }
}

此代码设置 Zorro 平台以训练和测试系统 1000 次。种子设置可确保您在任何 MRC 运行中获得相同的结果。从第二个周期开始，历史数据被打乱，没有替换。为了计算 p 值并绘制 MRC 的直方图，我们再次使用评估函数。它通过计算比原始系统更高的利润因子的回测来计算 p 值。根据系统的不同，使用 Zorro 训练和测试策略一千次需要几分钟时间。趋势跟踪系统的结果 MRC 直方图：

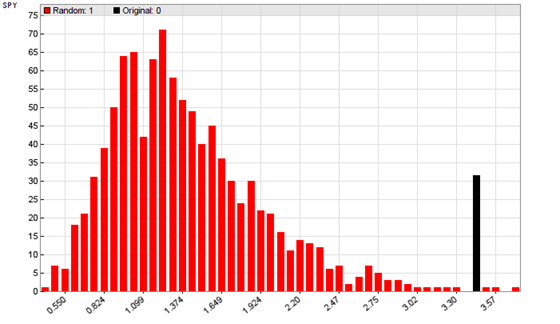
红色条的高度表示以 x 轴上显示的利润因子结束的混洗回测的数量。右边的黑条（高度无关，只有 x 轴位置重要）是原始价格曲线的利润因子。我们可以看到，由于 SPY 价格的长期上涨趋势，大多数洗牌测试结果都是正面的。但是我们的测试系统表现得更加积极。p 值低于 1%，这意味着我们的回测具有很高的意义。这给了我们一些信心，即简单的趋势跟踪器可以在实际交易中获得类似的结果。

这不能从安慰剂系统的 MRC 直方图中说出来：

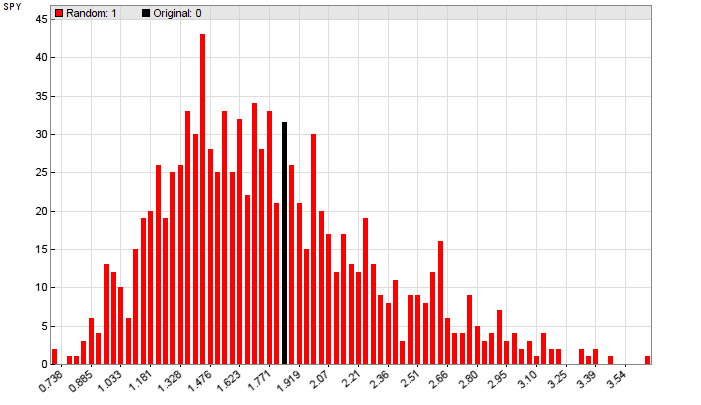
回测利润因子现在扩展到更广泛的范围，并且许多比原来的系统更有利可图。真实价格曲线的回溯测试与随机测试无法区分，p 值在 40% 区域。安慰剂系统的原始回测结果，即使通过前向分析实现，也因此毫无意义。

需要指出的是，MRC 无法检测到所有无效的回测。一个明确拟合特定价格曲线的系统，例如通过提前知道它的峰值和谷值，MRC 会得到一个低 p 值。没有任何现实检查可以将这样的系统与具有真正优势的系统区分开来。因此，无论是 MRC 还是 WRC 都不能绝对保证系统在通过检查时可以正常工作。但是当它没有通过时，建议您最好不要用真钱进行交易。

我已将策略上传到 2022 脚本存储库。MRC 和 WFOProfile 脚本包含在 Zorro 版本 2.47.4 及更高版本中。您将需要 Zorro S 来对安慰剂系统进行强力优化。